Βιοστατιστική (2061-2062)

Ορισμός της Βιοστατιστικής – Εισαγωγικές Έννοιες

Στόχοι Ενότητας

Γνωριμία με το γνωστικό αντικείμενο της Βιοστατιστικής, την χρησιμότητά του για τα επαγγέλματα υγείας καθώς και την αναγκαιότητα εκμάθησής του

Λέξεις Κλειδιά

Βιοστατιστική, Επιδημιολογία

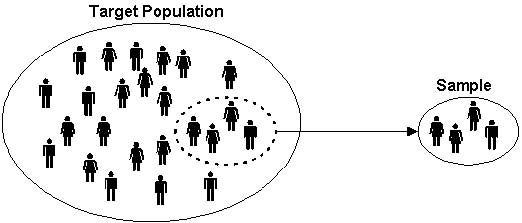Στην ενότητα αυτή, ο αναγνώστης εισάγεται στις βασικές έννοιες της Ιατρικής Στατιστικής ή  αλλιώς  Βιοστατιστικής. Συγκεκριμένα, στην ενότητα αυτή παρουσιάζονται  βασικές έννοιες της Στατιστικής όπως πληθυσμός και  δείγμα  καθώς επίσης και τα σημαντικότερα εργαλεία που χρησιμοποιεί η Ιατρική Στατιστική προκειμένου να συλλέξει σύνολα δεδομένων, τα οποία προέρχονται από σχετικούς µε την υγεία τομείς, όπως η ιατρική, η βιολογία, η επιδημιολογία και η υγιεινή προκειμένου να αναδείξει σχέσεις μεταξύ αυτών.

Στόχοι Ενότητας

Μελετώντας το υλικό της ενότητας αυτής θα είστε σε θέση να ξεχωρίζετε τον πληθυσμό από το δείγμα και να γνωρίζετε τις βασικές μεθόδους δειγματοληψίας.

Λέξεις Κλειδιά

Συλλογή Δεδομένων, Πληθυσμός, Δείγμα, Δειγματοληψία.

Αντικείμενο της ενότητας αυτής είναι η περιγραφική ανάλυση μιας ή περισσοτέρων ποσοτικών ή ποιοτικών μεταβλητών (ηλικία, βάρος, CRP, γGT, κτλ.). Οι τιμές μιας μεταβλητής, αξιοποιούμενες  μέσω περιγραφικών μέτρων και διαγραμμάτων, παρέχουν σημαντικές πληροφορίες για τον πληθυσμό από τον οποίο προέρχεται το δείγμα μας.

Στην ενότητα αυτή θα ασχοληθούμε με πίνακες συχνοτήτων δεδομένων, τον υπολογισμό και ερμηνεία κατάλληλων περιγραφικών μέτρων (μέση τιμή, διακύμανση, τυπική απόκλιση κτλ) και διαγραμμάτων (ιστόγραμμα, πολύγωνο συχνοτήτων, box plot). Επιπλέον θα παρουσιασθούν οι πίνακες συχνοτήτων και κατάλληλα διαγράμματα, όπως τα ραβδογράμματα και τα κυκλικά διαγράμματα, που χρησιμοποιούνται στην περίπτωση μιας ποιοτικής μεταβλητή (φύλο, τύπος επέμβασης, θεραπευτική ομάδα κτλ).

Στόχοι Ενότητας

Μελετώντας το υλικό της ενότητας αυτής θα είστε σε θέση να ξεχωρίζετε τα είδη των μεταβλητών (ποσοτικές και ποιοτικές). Επίσης θα είστε σε θέση να αναγνωρίζετε την κλίμακα μέτρησης (ονομαστική, διατάξιμη, διαστήματος, λόγου) των μεταβλητών σας. θα μπορείτε να περιγράφετε τα δεδομένα που έχετε συλλέξει. Πιο συγκεκριμένα θα γνωρίζετε πως να ομοδοποιείτε τα δεδομένα και να κατασκευάζετε κατάλληλους πίνακες συχνοτήτων, να υπολογίζετε και να ερμηνεύετε περιγραφικά μέτρα (μέση τιμή, διακύμανση, τυπική απόκλιση κτλ) και να κατασκευάζετε κατάλληλα διαγράμματα (ιστόγραμμα, πολύγωνο συχνοτήτων, box plot).

Λέξεις Κλειδιά

Μέτρα θέσης, Μέτρα διασποράς, Διαγράμματα, Πίνακες Συχνοτήτων, Μεταβλητές.

Αντικείμενο της ενότητας αυτής είναι η εισαγωγή στην έννοια της Πιθανότητας και της Δεσμευμένης Πιθανότητας.

Στόχοι Ενότητας

Μελετώντας το υλικό της ενότητας αυτής θα είστε σε θέση να κατανοήσετε βασικές έννοιες της πιθανότητας και της δεσμευμένης πιθανότητας και να επιλύετε ασκήσεις υπολογισμού τους.

Λέξεις Κλειδιά

Δειγματικός Χώρος, Πιθανότητα, Δεσμευμένη Πιθανότητα.

Στην ενότητα αυτή θα μας απασχολήσουν βασικές έννοιες  όπως της τυχαίας μεταβλητής, της συνάρτησης πυκνότητας  πιθανότητας  καθώς και της συνάρτησης κατανομής της. Επίσης μας ενδιαφέρουν οι βασικές συνεχείς και διακριτές κατανομές.

Στόχοι Ενότητας

Μελετώντας το υλικό της ενότητας αυτής θα είστε σε θέση να κατανοήσετε την τυχαία μεταβλητή,  της συνάρτησης πυκνότητας  πιθανότητας  καθώς και τη συνάρτησης κατανομής μιας τμ. Επίσης θα είστε σε θέση να υπολογίζετε τη μέση τιμή και διακύμανσή της καθώς και να χειρίζεστε  βασικές συνεχείς και διακριτές κατανομές όπως η κανονική, η ομοιόμορφη, η εκθετική, η διωνυμική, η Poisson κα .

Λέξεις Κλειδιά

Τυχαίες μεταβλητές, Συνεχείς Κατανομές, Διακριτές Κατανομές, Μέση Τιμή Τ.Μ. Διακύμανση Τ.Μ.

Συγκεκριμένα στην ενότητα αυτή θα μας απασχολήσει η συμπερασματολογία για ένα ή δύο ανεξάρτητα δείγματα μέσω της κατασκευής κατάλληλων διαστημάτων εμπιστοσύνης και ελέγχων υποθέσεων. Αντικείμενο της ενότητας  αυτής, επίσης  είναι η ανάλυση ποσοτικών μεταβλητών που προέρχονται από εξαρτημένα δείγματα. Δυο δείγματα θεωρούνται εξαρτημένα όταν έχουμε φυσικά ή ταιριασμένα (paired) δείγματα. Για παράδειγμα, καταγράφουμε τα επίπεδα χοληστερόλης σε ζεύγη συγγενών ή σε ζεύγη ασθενών και μαρτύρων. Ιατρικό ενδιαφέρον έχει να ελέγξουμε εάν τα επίπεδα χοληστερόλης διαφέρουν μεταξύ των δυο δειγμάτων.

Στόχοι Ενότητας

Μελετώντας το υλικό της ενότητας αυτής θα είστε σε θέση να εξέγετε συμπεράσματα που αφορούν την μέση τιμή ενός πληθυσμού και τη διαφορά μέσων τιμών δύο πληθυσμών. Συγκεκριμένα, θα μπορείτε να κατασκευάζετε διαστήματα εμπιστοσύνης που θα περιέχουν την πραγματική τιμή της μέσης τιμής με συγκεκριμένη πιθανότητα και να διενεργείτε ελέγχους σχετικά με το εάν η μέση τιμή ενός πληθυσμού ισούται με μια συγκεκριμένη τιμή ή οι εάν οι  μέσες τιμές δύο πληθυσμών έχουν στατιστικά σημαντική διαφορά.

Λέξεις Κλειδιά

Μηδενική Υπόθεση, Εναλλακτική Υπόθεση, Έλεγχος Υποθέσεων, Διάστημα Εμπιστοσύνης, p-value, Μέγεθος Δείγματος, Ισχύς Ελέγχου, Σφάλμα Τύπου Ι,ΙΙ, t-test, paired t-test.

Σκοπός της ενότητας αυτής είναι η μελέτη της σχέσης που συνδέει τις μεταβλητές στην περίπτωση που έχουμε ποιοτικές. Για παράδειγμα μας ενδιαφέρει εάν υπάρχει σχέση ανάμεσα στο φύλο ενός ατόμου και στην εμφάνιση ή όχι εμφράγματος ή εάν υπάρχει σχέση ανάμεσα στην εμφάνιση του μικροβίου του έρπη με την εμφάνιση Αλτζχάιμερ κλπ

Στόχοι Ενότητας

Μελετώντας το εκπαιδευτικό υλικό αυτής της ενότητας, θα είστε σε θέση να διακρίνετε πότε πρέπει να χρησιμοποιείτε τους μη παραμετρικούς ελέγχους για να συγκρίνετε δύο ποιοτικά χαρακτηριστικά. Επιπλέον θα είστε σε θέση να εφαρμόζετε τους ελέγχους αυτούς και να ερμηνεύετε τα αποτελέσματά τους.

Λέξεις Κλειδιά

Μη παραμετρικοί έλεγχοι, Έλεγχος Χ²

Σκοπός της ενότητας αυτής είναι η μελέτη της σχέσης που συνδέει τις μεταβλητές. Για παράδειγμα μας ενδιαφέρει εάν υπάρχει σχέση ανάμεσα στο βάρος ενός ατόμου και στο δείκτη μάζας σώματος ή εάν υπάρχει σχέση ανάμεσα στην παχυσαρκία και στις ώρες παρακολούθησης τηλεόρασης. Στην περίπτωση αυτή έχουμε δυο ποσοτικές μεταβλητές και η σχέση μεταξύ τους ονομάζεται συσχέτιση. Από τη στιγμή που έχουμε διαπιστώσει ότι υπάρχει γραμμική σχέση μεταξύ μεταβλητών έχει ενδιαφέρον να βρούμε ένα μοντέλο που συνδέει αυτές τις μεταβλητές με απώτερο σκοπό την πρόβλεψη της μιας από τις τιμές των άλλων. Για παράδειγμα ο ιατρικός ερευνητής ενδιαφέρεται να εκτιμά το βάρος του ατόμου από τη μάζα λίπους του. Αυτό επιτυγχάνεται μέσω της Ανάλυσης Παλινδρόμησης (Regression Analysis).

Στόχοι Ενότητας

Μελετώντας το εκπαιδευτικό υλικό αυτής της ενότητας, θα είστε σε θέση να ξεχωρίζετε τις έννοιες συσχέτιση και συνάφεια. Επιπλέον θα μπορείτε να υπολογίζετε και να αξιολογείτε τον παραμετρικό συντελεστή γραμμικής συσχέτισης του Pearson και τον μη παραμετρικό συντελεστή συσχέτισης του Spearman που αφορούν τη συσχέτιση ποσοτικών μεταβλητών. Επίσης, μελετώντας το υλικό της ενότητας αυτής θα είστε σε θέση να προσαρμόζετε το μοντέλο της απλής γραμμικής παλινδρόμησης, όταν έχετε μια μεταβλητή απόκρισης και μια ανεξάρτητη μεταβλητή καθώς και να μπορείτε να ελέγχετε αν υπάρχει συσχέτιση μεταξύ δύο μεταβλητών.

Λέξεις Κλειδιά

Συσχέτιση, Παλινδρόμηση, Pearson, Spearman.

Αντικείμενο της ενότητας αυτής είναι η ανάλυση ποσοτικών μεταβλητών που προέρχονται από περισσότερα των δύο ανεξάρτητα δείγματα. Δυο δείγματα θεωρούνται ανεξάρτητα όταν οι τιμές του ενός δεν εξαρτώνται / σχετίζονται με τις τιμές του άλλου. Για παράδειγμα, καταγράφουμε τον αριθμό των λευκών αιμοσφαιρίων ανθρώπων με κάποιου είδους λοίμωξη και τον αντίστοιχο αριθμό υγιών ατόμων. Ιατρικό ενδιαφέρον έχει να ελέγξουμε εάν ο αριθμός των λευκών αιμοσφαιρίων διαφέρει μεταξύ των δυο ομάδων. Με την ίδια λογική είναι δυνατό να συγκρίνουμε την αποτελεσματικότητα δύο φαρμάκων ή δύο θεραπειών. Για παράδειγμα, μας ενδιαφέρει να μετρήσουμε εάν η ρύθμιση της πίεσης επιτυγχάνεται το ίδιο καλά με δύο διαφορετικά φάρμακα ή ακόμα μας ενδιαφέρει να δούμε την αποτελεσματικότητα ενός χειρουργείου με δύο διαφορετικές μεθόδους. Σε προηγούμενη ενότητα  παρουσιάσθηκε η περίπτωση που έχουμε δυο ανεξάρτητα δείγματα ενώ εδώ θα παρουσιασθεί η περίπτωση που έχουμε περισσότερα από δυο δείγματα. Θα παρουσιασθεί ο κατάλληλος παραμετρικός έλεγχος με  δεδομένα που ακολουθούν την κανονική κατανομή.

Στόχοι Ενότητας

Μελετώντας το εκπαιδευτικό υλικό αυτής της ενότητας, θα είστε σε θέση να διακρίνετε πότε πρέπει να χρησιμοποιείτε τους παραμετρικούς ελέγχους και πότε τους μη παραμετρικούς ελέγχους για να συγκρίνετε τις μέσες τιμές περισσοτέρων των δύο ανεξάρτητων δειγμάτων. Επιπλέον θα είστε σε θέση να εφαρμόζετε τους  παραμετρικούς ελέγχους  αυτούς και να ερμηνεύετε τα αποτελέσματά τους.

Λέξεις Κλειδιά

ANOVA, Έλεγχος Υποθέσεων, p-value, Post Hoc Analysis.